Functions, Limits, Continuity (part 4)
Posted by Unknown on 5:53 AM with No comments
Problems for "Continuity".
Problem :
Is
f (x) = x
3 + 2x + 1
continuous at
x = 2
?
Yes. All polynomial functions are continuous. To check,
Yes. All polynomial functions are continuous. To check,
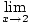 f (x) = 13 and f (2) = 13
f (x) = 13 and f (2) = 13
|
Problem :
Is
f (x) = 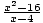 continuous at
x = 4
?
continuous at
x = 4
?
No. f (4) is undefined.
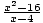 continuous at
x = 4
?
continuous at
x = 4
?No. f (4) is undefined.
Problem :
Is the following function continuous?
Since this function is a junction of two continuous functions, we only have to worry about discontinuity at the point where the functions meet, i.e. at x = 2 .
Thus, f (x) = 5
,
and
f (2) = 5
, so
f (x) = 5
,
and
f (2) = 5
, so
 f (x) = f (2)
. It follows that
f
is continuous.
f (x) = f (2)
. It follows that
f
is continuous.
f (x) = 
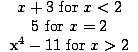
|
Since this function is a junction of two continuous functions, we only have to worry about discontinuity at the point where the functions meet, i.e. at x = 2 .
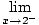 f (x)
f (x) |
= 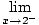 x + 3 = 2 + 3 = 5
x + 3 = 2 + 3 = 5 |
||
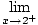 f (x)
f (x) |
= 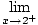 (x
4 -11) = 24 - 11 = 5 (x
4 -11) = 24 - 11 = 5 |
Thus,
 f (x) = 5
,
and
f (2) = 5
, so
f (x) = 5
,
and
f (2) = 5
, so
 f (x) = f (2)
. It follows that
f
is continuous.
f (x) = f (2)
. It follows that
f
is continuous.
Problem :
Is the following function continuous?
Since this function is a junction of two continuous functions, we only have to worry about discontinuity at the point where the functions meet, i.e. at x = 3 .
Since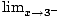 f (x)≠
f (x)≠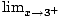 f (x),
f (x),
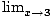 f (x)
does not exist, and
f
is not continuous at
x = 3.
f (x)
does not exist, and
f
is not continuous at
x = 3.
f (x) = 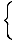
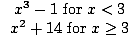
|
Since this function is a junction of two continuous functions, we only have to worry about discontinuity at the point where the functions meet, i.e. at x = 3 .
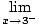 f (x)
f (x) |
= 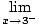 (x
3 -1) = 33 - 1 = 26 (x
3 -1) = 33 - 1 = 26 |
||
| lim x→3+ f (x) | = 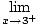 (x
2 +14) = 32 + 14 = 23 (x
2 +14) = 32 + 14 = 23 |
Since
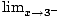 f (x)≠
f (x)≠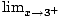 f (x),
f (x),
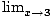 f (x)
does not exist, and
f
is not continuous at
x = 3.
f (x)
does not exist, and
f
is not continuous at
x = 3.
Problem :
Is there a way to define
f (c)
for the following function so that
f (x)
is continuous at
x = c
?
Because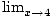 f (x) = 8
, we should define
f (4) = 8
to make this function continuous.
f (x) = 8
, we should define
f (4) = 8
to make this function continuous.
f (x) = 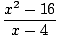 at c = 4 at c = 4
|
 f (x)
f (x) |
= 
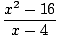
|
||
= 
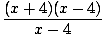
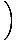
|
|||
=  (x + 4) (x + 4) |
|||
| = 8 |
Because
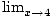 f (x) = 8
, we should define
f (4) = 8
to make this function continuous.
f (x) = 8
, we should define
f (4) = 8
to make this function continuous.
Problem :
Is there a way to define
f (c)
for the following function so that
f (x)
is continuous at
x = c
?

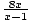 = - ∞
(the numerator approaches 8 and the denominator becomes an
extremely
small negative number, so the limit goes to
- ∞
)
= - ∞
(the numerator approaches 8 and the denominator becomes an
extremely
small negative number, so the limit goes to
- ∞
)
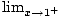
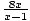 = + ∞
(the numerator approaches 8 and the denominator becomes an
extremely
small positive number, so the limit goes to
+ ∞
)
This means that
= + ∞
(the numerator approaches 8 and the denominator becomes an
extremely
small positive number, so the limit goes to
+ ∞
)
This means that
 f (x)
doesn't exist, so there
is no way to
define
f (1)
to make
f
continuous.
f (x)
doesn't exist, so there
is no way to
define
f (1)
to make
f
continuous.
f (x) = 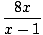 at x = 1 at x = 1
|

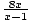 = - ∞
(the numerator approaches 8 and the denominator becomes an
extremely
small negative number, so the limit goes to
- ∞
)
= - ∞
(the numerator approaches 8 and the denominator becomes an
extremely
small negative number, so the limit goes to
- ∞
)
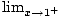
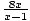 = + ∞
(the numerator approaches 8 and the denominator becomes an
extremely
small positive number, so the limit goes to
+ ∞
)
This means that
= + ∞
(the numerator approaches 8 and the denominator becomes an
extremely
small positive number, so the limit goes to
+ ∞
)
This means that
 f (x)
doesn't exist, so there
is no way to
define
f (1)
to make
f
continuous.
f (x)
doesn't exist, so there
is no way to
define
f (1)
to make
f
continuous.
Problem :
How can we be sure that the function
f (x) = 3x
3 -2x
2 - 31
has a root on the interval
[0, 3]
?
We can use the intermediate value theorem. Because f is a polynomial function, it is continuous. f (0) = - 31 and f (3) = 32 . Since 0 lies between f (0) and f (3) , the intermediate value theorem tells us that there is at least one c on [0, 3] for which f (c) = 0 . In other words, f has a root on [0, 3] .
We can use the intermediate value theorem. Because f is a polynomial function, it is continuous. f (0) = - 31 and f (3) = 32 . Since 0 lies between f (0) and f (3) , the intermediate value theorem tells us that there is at least one c on [0, 3] for which f (c) = 0 . In other words, f has a root on [0, 3] .


0 comments:
Post a Comment